
Quantum Entanglement
Source of entangled photons
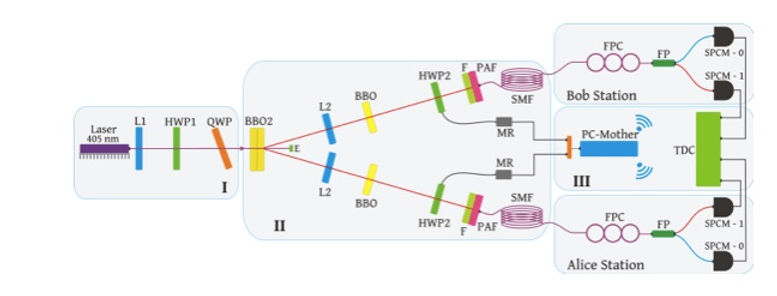
Scheme of the current QKD setup, which is a realization of the Bell’s experiment. Sector I: pump. Sector II: source of entangled photons. Sector III: acquisition and control. L1: plano-convex lens (f = 300 mm), HWP1: half-waveplate (λ = 404.6 nm), QWP: quarter-waveplate (λ = 405 nm), BBO2: two crossed BBO-I crystals (θ = 28.9º, φ = 0º, size: 5×5×0.9 mm3), L2: convex lens (f = 300 mm), BBO: (θ = 28.9º, φ = 0º, size: 5×5× 0.45 mm3), HWP2: half-waveplate (λ =810 nm) mounted in a motorized rotation stage, MR: Servo motor controller, F: bandpass filter ((λ = 810 nm, FWHM = 10 nm), PAF: fiberport (f = 7.5 mm), SMF: 50 m of single-mode fiber coil, TDC: time-to-digital converter (4 channels) record time values of photons’ detection with 10 ps precision, FPC: birefringence compensator, FP: fiber polarization beam splitter, SPCM: photon counting module. The PC-Mother manages the automatic naming, opening and closing of recorded files in the TDC through a wifi link.

A) Laptop with time stamping software ; B) TDC IDQ900; C) SPCM 1 & 2 ; D) Motorized rotation stage
Testing how different levels of entanglement affect predictability in practical setups
The generation of series of random numbers is an important and difficult problem. Appropriate measurements on entangled states have been proposed as the definitive solution. In principle, this solution requires reaching the challenging “loophole-free” condition, which is unattainable in a practical situation nowadays. Yet, it is intuitive that randomness should gradually deteriorate as the setup deviates from that ideal condition. In order to test whether this trend exists or not, we prepare biphotons with three different levels of entanglement: moderately entangled (S=2.67), marginally entangled (S=2.06), and non-entangled (S=1.42) in a setup that mimics a practical situation. The indicators of randomness we use here are: a battery of standard statistical tests, Hurst exponent, an evaluator of Kolmogorov complexity, Takens’ dimension of embedding, and augmented Dickey–Fuller and Kwiatkowski–Phillips–Schmidt–Shin to check stationarity. A nonparametrical statistical ANOVA (Kruskal–Wallis) analysis reveals a strong influence of the level of entanglement with randomness when measured with Kolmogorov complexity in three time series with P-values and strength factor ϵ2: P=0.0015, ϵ2=0.28; P=4.5×10−4, ϵ2=0.67 and P=5.6×10−4, ϵ2=0.16. The setup is pulsed with time stamping, what allows generate different series applying different methods with the same data, even after the experimental run has ended, and to compare their raw randomness. It also allows the stroboscopic reconstruction of time variation of entanglement.